「上に凸」の生存曲線の不自然さを熟考する

前回、故・近藤誠先生が提唱された「がん放置療法」の中で、

「がん医療の中で抗がん剤治療の延命効果について調査した医学論文には人為的介入の可能性がある」というご意見には一考の価値があるということを述べました。

その人為的介入の有無を疑うポイントとして『生存曲線が「上に凸」の形を示していること』を近藤先生は指摘されています。

正直私は近藤先生にそのことを指摘されるまでは、生存曲線の形には何の注目もしていませんでした。だからこそがん医療の医学論文に特段の問題を見出すことができなかったとも言えます。

しかしこの近藤先生が指摘された「上に凸」生存曲線問題について深く考察していくと、おそらくまだがん医療の中で誰も指摘していないであろう問題点が浮かび上がってきました。

グラフの形という細かくてややこしい話を深掘りするということで興味をひきにくい話題に思えるかもしれませんが、結論は誰にとっても関係のある重大な内容になってきます。

長くなってしまい大変恐縮ですが、なるべくわかりやすい説明を心がけてみますので、是非とも最後までお読み頂ければ幸いです。 まず生存曲線について簡単におさらいしますが、生存曲線というのは横軸に時間、縦軸に生存率を設定し、

グラフ左上の年間生存率（※1年間でどのくらいの割合の人が生存しているか。以下「生存率」と表現する）が100%で時間0（まだ時間が経っていない）の状態からスタートして、右に移動して時間が経過していくにつれて亡くなる人が出て、生存率がどのように下がっていくかについて表現された曲線上のグラフとなります。

厳密には曲線ではなく、時間経過とともに亡くなる人が現れるまではグラフの線は右側へ水平に移動し、亡くなった人が現れた時点でグラフはその人数分だけ生存率が下がるよう垂直に移動し、また次の人が亡くなるまで水平移動し、次の人が亡くなったら垂直移動するというように、曲線のような細かい階段状のグラフを示すことになります。前回記事でも言いましたが、このような形で生存曲線を表現する方法のことを「カプラン・マイヤー法（KM法）」と言います。


（画像はこちらのサイトより引用）

上記はカプランマイヤー法で表現された生存曲線の架空の例ですが、点線のグラフは「上に凸」の形を、実線のグラフは「下に凸」の形をしていると思います。

それもそのはず、ある治療法を行なってどの時点でその人が亡くなるかは個人差があって、年齢、人種、既往歴などの背景も違えばどの時点で人が亡くなるかなんてことは全く予想できないわけですから、グラフが「上に凸」になるか「下に凸」になるかはわからないという点には何の疑問も持たないのではないでしょうか。

しかし、これを調べる対象が集団として大きくなっていけば、話が変わってきます。例えば、とあるがん患者の集団を考えてみます。

ここで考えるがん患者集団というのは、がん患者であれば誰でもよいわけではなく、特定の臓器のがんに絞られ、年齢もがんの進行度も同じくらいの人達がたくさん集まった集団を想定します。

そうした人が数人しか集まらなければ、集めた人によって年間死亡率（※1年間にどのくらいの割合の人が死亡するか。以下「死亡率」と表現する）が大きく変動することもあると思いますが、

同じような人を何百人も何千人も集めていくと、その特徴を持った人達の平均的な死亡率に収束していくことになります。一般的には集団が多くなればなるほどその特徴は「正規分布」を示すと言われています。


さて、もしも集団の死亡率がおよそ一定なのだと仮定した場合の話です。

近藤先生は『死亡率が一定の集団における生存曲線は「下に凸」の形の指数関数曲線になる』という説を、1986年に「Cancer」というがん医療業界における最高峰の医学雑誌に乗ったとある論文を引用しながら提唱されます（Harris JR, et al. Cancer 1986; 57: 925-928）。


（画像はHarris JR, et al. Cancer 1986; 57: 925-928より引用）

これはがん患者集団の死亡率が25%だと仮定した場合に（A）のような生存曲線を示すということ、（B）は縦軸を逆対数にすれば直線になるということを示すことで、これが死亡率一定集団の生存曲線の基本型になるということを示しています。

これが何も介入を加えないある特徴を持った集団の基本型だとすれば、これに何かしらの治療を加えた場合にはどうなるのでしょうか。同論文に次のような図も示されています。


（画像はHarris JR, et al. Cancer 1986; 57: 925-928より引用）

これは乳がんの患者に手術を行なって、長期生存率がどうなったかを30年以上追いかけた2つの研究の結果を示した生存曲線になります。

先ほどのグラフが理論値だとすれば、こちらのグラフは実測値ということになります。それにしても30年以上も追いかけたデータはなかなか貴重ですね。

ただ調査したポイントが少ないので曲線というよりは折れ線を示してはいます。それでもやはり下に凸の曲線を模した形になっていることはわかります。

もう少し細かく見れば、10年のタイミングを境にして前後でグラフの傾きが変わっているように見えます。論文によれば10年より前の集団の死亡率は約10％、10年より以降の集団の死亡率は約2〜3％となっているようです。

ここでのポイントは『何か治療を加えた場合の死亡率は最初ぐっと下がるけれど、その死亡リスクを乗り越えた新たな集団では全体として死亡率が下がり、全体としての生存曲線はやはり「下に凸」の形を呈する』ということだと思います。

それが故に「抗がん剤の治療効果を見る医学論文で生存曲線が「上に凸」の形になるのは人為的操作の可能性がある」と近藤先生は主張しているわけです。

ちなみに死亡率25%と設定したからたまたま「下に凸」の生存曲線になるだけではないかという疑問に答えるために、

念の為、死亡率80%の集団のケース、死亡率5%の集団のケースをそれぞれ仮定してグラフを作ってみました。


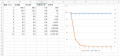
（画像は自作）


（画像は自作）

いずれのケースでも「上に凸」の形は示さないということがわかると思います。よって死亡率が一定であると仮定する限り、近藤先生の主張は理論上正しいということになると思います。


これに対して反論もあるわけですが、前回記事では腫瘍内科医の大場大先生の見解を紹介しました。

大場先生の見解は「手術を受けてから3〜4年経過するとがんが再発するリスクが高まるので、集団としての死亡率は時間が経過するにつれて高くなっていく」というものでした。

ただその話は先ほどの「Cancer」の医学論文の30年の実測データとずれてきます。大場先生の主張は「時間が経てば死亡率は高くなる」、「Cancer」論文の実測データは「時間が経てば死亡率は低くなる」を示し、主張と矛盾しているように思えます。

実は大場先生と同じような主張を自著の中で展開している先生がもう一人おられます。同じく腫瘍内科医の勝俣範之先生です。



「抗がん剤は効かない」の罪 単行本 – 2014/3/25
勝俣 範之 (著)

勝俣先生の「上に凸」生存曲線問題への主張も大場先生と同様で、上記の本にその辺りの話が詳しいのですが、勝俣先生はインターネット上でもその辺りを具体的に図を使いながら説明されていたので、ここではそれを紹介したいと思います。

要するに『どんな時にカプランマイヤー法での生存曲線は「上に凸」の形を示すのか』という問題を考える必要があるわけです。


まず勝俣先生は死亡率が一定の場合の生存曲線を次のように示されています。


（画像はこちらのサイトより引用）

Cancer論文の理論値と同様に生存曲線は「下に凸（指数関数曲線）」を示しています。

次に死亡率が徐々に下がっていく場合の生存曲線を次のように示されています。


（画像はこちらのサイトより引用）

こちらもやはり生存曲線は「下に凸」の形状を示しています。死亡率一定の場合よりも「下に凸」の凸具合が強く、後半になるにつれて平行線に近づいています。Cancer論文の実測値に近い形状ですね。

そしてもう一つ、死亡率が徐々に上昇していく場合の生存曲線を示しておられます。


（画像はこちらのサイトより引用）

このように、死亡率が徐々に上昇していく場合は「上に凸」の生存曲線を示すことがあると勝俣先生はシミュレーションで示されていました。

ただこの理論で行きますと、グラフが「上に凸」の形状を示すためには最初の死亡率が限りなくゼロに近い状態で推移しないと上に凸にならないのではないかと思い、

同じシミュレーションを私の方でも実施してみることにしました。

まずは勝俣先生と同様に初年度の死亡率を0%（＝生存率100%）と仮定して、年間2%ずつ死亡率が増加していくパターンの生存曲線です。


（画像は自作）

当然ながら勝俣先生と同様に「上に凸」の生存曲線になります。

では次に初年度の死亡率が10%（生存率=90%）と仮定し、年間2%ずつ死亡率が増加していくパターンの生存曲線です。


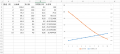
（画像は自作）

これだと「上に凸」とも「下に凸」とも言い難い形をしていますね。

そしてもう一つ、初年度の死亡率が20%（生存率=80%）と仮定し、年間2%ずつ死亡率が増加していくパターンの生存曲線を示します。


（画像は自作）

これだと徐々に死亡率が上昇していくパターンでありながら生存曲線は「下に凸」の形状を示しています。

つまり徐々に死亡率が上昇することは、生存曲線が「上に凸」の形状を示すための必要十分条件ではないということになります。

逆に言えば、生存曲線が『上に凸の形状を示すためには、死亡率が0%（生存率が100%）が近い状態をなるべく長くキープしておく必要がある』ということになると思います。

そうでないと「上に凸」になる場合の平坦な部分がまず形成されにくいということになるからです。

もう一つ「上に凸」の形状がグラフの途中で形成される可能性についてはどうでしょうか。

ちょっと強引ですが次のようなパターンをシミュレーションしてみました。


（画像は自作）

これは1年目と2年目の死亡率は10%で推移していたけれど、3〜8年目はなぜか死亡率が2％に急減し、9年目と10年目は死亡率が30%に増加したパターンです。このシミュレーションで途中に上に凸が現れるパターンを再現できています。

しかし考えて見ればわかるようにこれは極めて変な状況です。集団の死亡率が劇的に変動しています。しかも一方向ではなく、減少したかと思えば急激に増加するという不自然な変動の仕方です。

そう考えると、途中で「上に凸」になるパターンのグラフがいかに不自然であるかということになるのではないでしょうか。

つまりまとめるとこういうことです。生存曲線が「上に凸」の形状を呈するためには死亡率がほとんど変わらない状態を長時間維持しながら、同時にある時から急に死亡率が高くなる状況がある必要がある、ということだと思います。

しかも途中で「上に凸」になることは理屈上不自然（集団の死亡率が極端に変動し過ぎ）なので、自ずと「上に凸」の平坦部分を作るためには少なくとも最初の数年間死亡率をゼロに近い状態に保ち続けることがマストになってきます。

しかし自然集団でさえ10%とか25%という死亡率のがん患者の集団に対して、いくら抗がん剤が延命効果があると言っても最初の数年間死亡率ほぼ0%の状態をキープすることができますでしょうか。抗がん剤投与後に程なく亡くなってしまう人達のことを考えますとあまりにも実感と離れる話です。

勝俣先生は実際の医学論文を引き合いに出して、「死亡率が変動することは実際に起こりうる」と主張しておられます。それを示すのが次の論文の図表になります。


（画像はこちらのサイトより引用）

勝俣先生はこの論文で死亡率の変動が実際にあるのだとおっしゃっていますが、それは逆ではないでしょうか。

つまりカプラン・マイアー法で算出した生存曲線が先にできて、これから死亡率（→ハザード比）を算出したら右側のグラフのように変動を示したと。

言い換えれば、死亡率が変動したから「上に凸」になったのではなく、別の原因でグラフが「上に凸」になったから死亡率が変動しているように見えたと、

「上に凸」のグラフを作るためには、これくらいの死亡率が変動しないと成立しないということの逆証明であるように思えます。


さて、なぜ「上に凸」のグラフができるのかを考える上で、ここでカプランマイアー法における、とあるグラフ作成のルールを知っておくことが非常に重要になってきます。

もう一度、カプランマイアー法での生存曲線のサンプルを見てください。


（画像はこちらのサイトより引用）

点線グラフにも実線グラフにも途中で縦の線が入っている部分があると思います。

これは「打ち切り例」と言って、その段階で何らかの原因で調査の継続が困難となったということを意味する印です。

こちらのサイトによりますと、「打ち切り」になるのは大きく以下の4つのケースがあるそうです。

(1) 調査対象が、いなくなってしまう
生物であれば、檻などから逃げ出してしまい、調査不能になることがある。患者の場合は、転居などにより、通院先の病院を変えたために、調査が継続できなくなる場合がある。

(2) 死亡が発生しないまま、調査期間が終了する
通常、調査期間は、限られている。調査期間中に全ての個体が死亡するとは限らず、調査終了時に生存している個体が残存することが考えられる。

(3) 調査とは別の原因で死亡してしまう
例えば、がん患者を対象に抗がん剤の投与後の生存状況を調べていたところ、がんと無関係の急性心筋梗塞により、患者が死亡してしまうような場合がある。

(4) 調査の中止が必要となる場合がある
(3)の例と同様、がん患者を対象に抗がん剤の投与後の生存状況を調べていたところ、著しい副作用が生じたため、投与を中止することがある。これにより、調査も中止することとなる。

つまり「打ち切り例」はがん以外の原因で死んでいるかもしれないし、調査期間や方法の問題で打ち切りになっただけでどこかで普通に生きているのかもしれないわけですが、

ここが一番重要なところですが、「カプランマイヤー法では打ち切り例はその理由に関わらず、グラフ上は生存しているものとして扱われる」のです。

つまり原因はともかく、グラフの最初の方に打ち切り例が多く発生することがあれば、「上に凸」の形状を作るための死亡率ほぼ0%（生存率ほぼ100％）期間をグラフ状作ることができる、ということです。

そして実際の抗がん剤での生存曲線はどうなっているかと言いますと、例えば2014年のLacet oncologyという医学論文に掲載された悪性黒色腫に対するベラツフェニブという分子標的治療薬の効果を見た生存曲線を見てみます（Lancet Oncol. 2014 Mar; 15(3): 323-332.）。


（画像はLancet Oncol. 2014 Mar; 15(3): 323-332.より引用）

赤い線がベラツフェニブ投与群ですが、グラフ左上のスタート地点に打ち切り例が集中しており、その後しばらくほぼ生存率100%の平坦部分ができており、その結果グラフは「上に凸」の形状を示しています。

最初が肝心と言いますか、例えば最初のスタートが死亡率10%だったりしますと、上述のようにもうそれだけで「上に凸」のグラフになることは困難になりますので、最初が平坦になるかどうかは非常に重要な注目点になると思います。

ちなみに青い線がダカルバジンという悪性黒色腫に対する従来型（殺細胞型）の抗がん剤です。こちらはグラフ全体にまんべんなく打ち切り例が存在することで、「上に凸」とも「下に凸」とも判断しにくい微妙な形状を呈しています。しかしよく見れば打ち切り例が集中しているところがグラフが平坦になる傾向があることに気づくと思います。

赤い線のベラツフェニブは最初こそ打ち切り例が集中していましたが、その後はまばらになり、グラフの後半で打ち切り例が再び集中してここはまた平坦なグラフを呈しているという特徴の違いがあると思います。

このように打ち切り例はグラフの形状を大きく左右する要素となっていることがうかがえると思います。

近藤先生はこの打ち切り例が抗がん剤関連論文の人為的介入を作っていると述べられています。

例えば、抗がん剤の効果をよく見せるためには真面目に追跡調査をしなければ打ち切り例として扱うことができるので、見かけ上生存率が高まるように情報操作することもできるというそのような可能性を指摘しておられます。

ただ私はもちろんその可能性は否定はできないものの、全世界でそのような隠蔽工作が行われていると考えるのは、さすがに性悪説の立場に立ち過ぎのように思います。

多くのがん研究者達はおそらくルールに基づいて真面目に研究結果を出していると考えたいところです。私は陰謀論について考えるのは一番最後という立場をとっています。

では陰謀がないのであれば、真面目に研究をしていて、なぜグラフの最初に打ち切り例が集中して不自然な「上に凸」のグラフを形成してしまうのでしょうか。

ここからはおそらく今までに誰も指摘していない私の推測になりますが、

打ち切り例の4つの理由のうちの3つ目「調査とは別の原因で死亡してしまう」が深く関わっているのではないかと思います。

要するに生存曲線が下がるのは「がんが原因の死亡」の時だけなわけですが、逆に言えば「がんとは直接関係のない死亡」が起こってしまったら、それは「打ち切り例」、つまりグラフ上は生存のように扱われるということです。

ところで「がんで死ぬ」というのはどういう状態でしょうか。

実はこんな本があります。



「がん」では死なない「がん患者」 栄養障害が寿命を縮める (光文社新書) 新書 – 2016/5/19
東口 高志 (著)

この本の中には次のように書かれています。

（以下、p13より引用）

（前略）

実は、がん患者の死因を調べたデータでは、その8割近くががんそのものではなく、感染症で亡くなっているのです。

すなわち、がん患者の8割は、感染症で亡くなっているということです。

感染症には、食べ物などが誤って肺に入ったことで起こる誤嚥性肺炎、血液へばい菌が入ったことで起こる敗血症、カテーテルからばい菌が入ったことで起こるカテーテル敗血症など、さまざまなものがあります。

ではなぜ、8割ものがん患者が感染症にかかり、しかも亡くなってしまうのか？

ひと言で言えば、免疫機能が低下しているからです。そして、免疫機能の低下は、栄養障害によってもたらされます。

（引用、ここまで）

このデータの信頼性（本当に8割かどうか）は別にしても、ポイントは「がんが直接の死因だと言い切ることは意外と難しい」ということです。

がん患者が治療の末に誤嚥性肺炎で亡くなった場合、それはがんで亡くなったとも、感染症で亡くなったとも受け取ることができると思います。

ですが今、もし自分が新しい抗がん剤の治験に携わっている立場の医師だと仮定してみましょう。二重盲検といって医師側からは新しい抗がん剤を使っているのか、古い抗がん剤を使っているのか、どちらであるかはわからない状態ですが、

新しい抗がん剤の効果を検証する立場にいるという医師を持って研究に参加していると思います。

そんな状況で例えば、ある患者さんが抗がん剤投与後まもなく肺炎を起こして亡くなるという状況に遭遇したとします。

この医師はこの患者さんをがんが原因で亡くなったと判断するでしょうか、それとも肺炎（感染症）で亡くなったと判断するでしょうか。

おそらくこれは後者なのではないでしょうか。その立場でこの死亡をがんによる死亡だと判断する医師はいないであろうことは想像に難くありません。

と、いうことはですよ。新規抗がん剤のグラフの最初に集中している打ち切り例は、実際には最初にたくさん死んでいるにも関わらず、「他病死（がん以外の原因による死亡）」での「打ち切り例」と判断されてしまい、

実際には初期にたくさん亡くなっている状況があるにも関わらず、グラフ上はむしろ生存率の高い状態として反映されている可能性があるということです。

しかもその状況を治験にあたっている現場の医師も、治験を統括するコーディネーターの立場の医師も、誰もその状況を知らないということになってしまいます。

そう考えると、抗がん剤に延命効果があるという医学論文が量産され続けることに説明がつきますし、

恐ろしいことに真実は逆なのかもしれないという説に一定の説得力を生むように思います。

そしてがん医療を専門とする医師達がその事実に誰一人気づいていないことにも説明がつきます。

この誰にも気づかれない事実の神隠しを疑う唯一の手がかりが「上に凸」の生存曲線だということです。



……いかがでしょうか。まだ検討の余地はあるとは思いますが、十分あり得るストーリーではないでしょうか。

よくがん医療の専門家はこのような言い方をされることがあります。

「もしも抗がん剤が有害なのだとしたら、世界的な大事件であり、直ちに認可を取り消して然るべき事態だ。しかし実際には信頼度の高い（エビデンスレベルが高い）論文がこれまでに世界中で数えきれないくらい蓄積されてきている。だとしたらそんな大それたことが事実であるはずがない」

しかし、ワクチンの医学論文、糖質制限の医学論文も検証してきたことからもわかるように、

「エビデンスレベルの高いRCT（ランダム化比較試験）は信頼度が高い」「複数のRCTを統合したメタアナリシスは信頼度が高い」という論法は既に崩壊しています。

そしてエビデンスが高い論文が蓄積されているのに事実がそれを反映しないという状況が起こるとしたら一つだけ考えられる可能性があります。

それは「従来の常識が間違っていた場合」です。

これであれば専門家が誤り続けることも説明可能です。ワクチン、糖質制限、がん医療で同じ構造が起こっているように私には思えます。

その可能性が確からしく浮上してきた以上、この可能性について真摯に向き合い、検討することが、

科学者たる医師として取るべき行動ではないかと私は思います。


たがしゅう

関連記事

• 「上に凸」の生存曲線の不自然さを熟考する (2022/09/28)